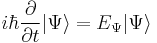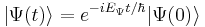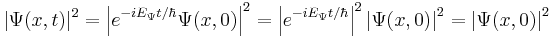Stationary state

In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time ^[1]. This corresponds to a quantum state with a single definite energy (instead of a probability distribution of different energies). It is also called energy eigenvector, energy eigenstate, energy eigenfunction, or energy eigenket. It is very similar to the concept of atomic orbital and molecular orbital in chemistry, with some slight differences explained below.

1 Introduction
2 Stationary state properties
3 Spontaneous decay
4 Comparison to "orbital" in chemistry
5 References
6 Sources
7 See also

Introduction

A stationary state is called stationary because a particle remains in the same state as time elapses, in every observable way. It has a constant probability distribution for its position, its velocity, its spin, etc.^[2] (This is true assuming the rest of the system is also static, i.e. the Hamiltonian is unchanging in time.) The wavefunction itself is not stationary: It continually changes its overall complex phase factor, so as to form a standing wave. The oscillation frequency of the standing wave, times Planck's constant, is the energy of the state according to the de Broglie relation.

Stationary states are quantum states that are solutions to the time-independent Schrödinger Equation:

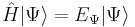$\hat H |\Psi\rangle=E_{\Psi} |\Psi\rangle$ ,

where

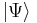$|\Psi\rangle$ is a quantum state, which is a stationary state if it satisfies this equation;
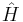$\hat H$ is the Hamiltonian operator;
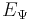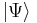$E_{\Psi}$ is a real number, and corresponds to the energy eigenvalue of the state $|\Psi\rangle$ .

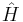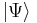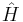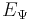This is an eigenvalue equation: $\hat H$ is a linear operator on a vector space, $|\Psi\rangle$ is an eigenvector of $\hat H$ , and $E_{\Psi}$ is its eigenvalue.

If a stationary state 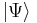$|\Psi\rangle$ is plugged into the time-dependent Schrödinger Equation, the result is ^[3]:

$i\hbar\frac{\partial}{\partial t} |\Psi\rangle = E_{\Psi}|\Psi\rangle$

Assuming that 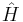$\hat H$ is time-independent (unchanging in time), this equation holds for any time t. Therefore this is a differential equation describing how 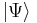$|\Psi\rangle$ varies in time. Its solution is:

$|\Psi(t)\rangle = e^{-iE_{\Psi}t/\hbar}|\Psi(0)\rangle$

Therefore a stationary state is a standing wave that oscillates with an overall complex phase factor, and its oscillation angular frequency is equal to its energy divided by 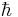$\hbar$ .

Stationary state properties

As shown above, a stationary state is not mathematically constant:

$|\Psi(t)\rangle = e^{-iE_{\Psi}t/\hbar}|\Psi(0)\rangle$

However, all observable properties of the state are in fact constant. For example, if 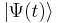$|\Psi(t)\rangle$ represents a simple one-dimensional single-particle wavefunction 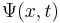$\Psi(x,t)$ , the probability that the particle is at location x is:

$|\Psi(x,t)|^2 = \left| e^{-iE_{\Psi}t/\hbar}\Psi(x,0)\right|^2 = \left| e^{-iE_{\Psi}t/\hbar}\right|^2 \left| \Psi(x,0)\right|^2 = \left|\Psi(x,0)\right|^2$

which is independent of the time t.

The Heisenberg picture is an alternative mathematical formulation of quantum mechanics where stationary states are truly mathematically constant in time.

As mentioned above, these equations assume that the Hamiltonian is time-independent. This means simply that stationary states are only stationary when the rest of the system is fixed and stationary as well. For example, a 1s electron in a hydrogen atom is in a stationary state, but if the hydrogen atom reacts with another atom, then the electron will of course be disturbed.

Spontaneous decay

Spontaneous decay complicates the question of stationary states. For example, according to simple (nonrelativistic) quantum mechanics, the hydrogen atom has many stationary states: 1s, 2s, 2p, and so on, are all stationary states. But in reality, only the ground state 1s is truly "stationary": An electron in a higher energy level will spontaneously emit one or more photons to decay into the ground state. This seems to contradict the idea that stationary states should have unchanging properties.

The explanation is that the Hamiltonian used in nonrelativistic quantum mechanics is only an approximation to the true Hamiltonian of the universe. The higher-energy electron states (2s, 2p, 3s, etc.) are stationary states according to the approximate Hamiltonian, but not stationary according to the true Hamiltonian, because of vacuum fluctuations. On the other hand, the 1s state is truly a stationary state, according to both the approximate and the true Hamiltonian.

Comparison to "orbital" in chemistry

Main articles: Atomic orbital and Molecular orbital

In chemistry, a stationary state of an electron is called an orbital; more specifically, an atomic orbital for an electron in an atom, or a molecular orbital for an electron in a molecule. However, there are some differences between "orbital" and "stationary state". First, when there is no spin-orbit coupling, there will be pairs of stationary states with the same configuration in space, but with opposite electron spin. These two states are considered to be just one orbital; therefore the Pauli exclusion principle allows two electrons per orbital, but only one electron per stationary state. Second, an orbital is usually a wavefunction describing just one electron, even though the true stationary state is a many-particle state requiring a more complicated description (such as a Slater determinant of individual orbitals). In this case an orbital is only approximately a stationary state.

References

^ Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, ISBN(10) 0 07 145546 9
^ Cohen-Tannoudji, Claude, Bernard Diu, and Franck Laloë. Quantum Mechanics: Volume One. Hermann, 1977. p. 32.
^ Quanta: A handbook of concepts, P.W. Atkins, Oxford University Press, 1974, ISBN 0-19-855493-1

Sources

Stationary states, Alan Holden, Oxford University Press, 1971, ISBN 19-851121-3